Understanding MPI Reduction Algorithms
- 0 Collaborators
A look into MPI Reduce operations both basic and complex. ...learn more
Overview / Usage
Collective communication functions defined by the Message Passing Interface are often used
in high performance computing workflows to orchestrate collective actions amongst groups of
processes. The reduce operation is useful when developers need to combine data stored at each
MPI process. Current reduce implementations are highly optimized to minimize the operation’s
execution time while maximizing network and process utilization. This paper explores three
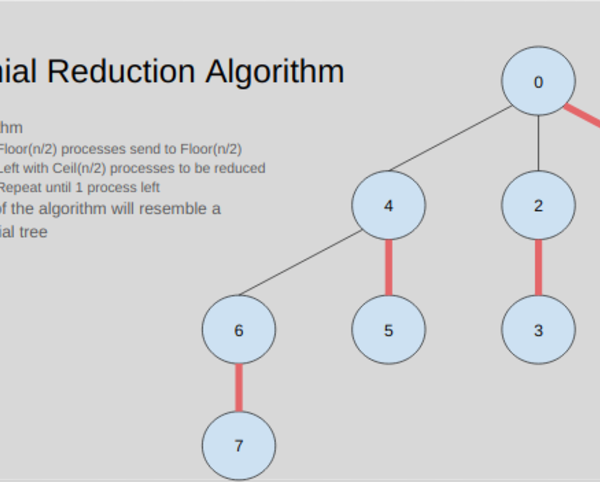
basic approaches: binomial, pipelined, and pipelined binary tree reductions. Both theoretical
and empirical running times are discussed regarding these algorithms. Modern reduce algorithms
utilize these basic approaches and captilize on their strengths. This paper also analyzes a new
greedy pipelined reduction algorithm and empirically benchmarks it against current approaches.
Findings show that binomial reductions are faster for smaller messages while pipelined and
pipelined binary tree implementations are faster for larger messages. Furthermore, the greedy
pipelined algorithm can be faster in all situations, however requires that an optimal message
segment size be chosen.